参考資料

Spherical Indexing

はじめに

Dictionary Indexingは、電子後方散乱回折（EBSD）の実測パターンを、方位空間の均一な格子上の各方位のシミュレーションパターンのディクショナリーと比較します[1,2]。合成パターンは、結晶方位によって菊池パターン球面を回転させ、実際のジオメトリを使用して平面に投影することによって生成されます。物理ベースのフォワードモデルとの比較により、優れた精度とノイズ耐性が得られますが、その代わりに計算量が大幅に増加します。Spherical Indexingでは、同じ菊池パターン球面または「マスターパターン」を使用しますが、代わりに球面上に実験パターンを逆投影します。方位は、逆投影されたパターンと菊池パターン球面間の最大球面相互相関を使用して、指数付けされます[3,4]。数学的には、Dictionary IndexingとSpherical Indexingは非常によく似ていますが、球面アプローチの方が、計算に高速フーリエ変換を利用できるため、より効率が上がります。実際には、Spherical IndexingはDictionary Indexingと同様の精度[5]とノイズ耐性を持ちながら、より高速な処理を実現しています。

OIM Matrix™モジュールの一部としてOIM Analysis™に実装されたEBSD Spherical Indexingは、数百または数千パターン/秒の優れた指数付けクオリティーを提供します。ここでは、様々なスキャンにこれを適用し、指数付けとユーザーパラメーターを実証しました。

Spherical Indexingには、バンド幅とグリッドサイズという2つのパラメーターがあります。バンド幅は、周波数空間における高調波を計算する距離です（EBSDパターンのローパスフィルターに相当します）。グリッドサイズは、相関に使用される（グリッドサイズ）のオイラー角の立方体との相関分解能です（例えば、phi1、Phi、およびphi2について0〜360）。一般的に、計算時間はオイラー角の格子点の数に比例し、妥当なバンド幅は格子点サイズの半分未満です。たとえば、次のような合理的な値の組があります。

Bandwidth	Grid Size
63	128
95	192
127	256

最適なオイラーグリッドポイント (最大の相互相関) が選択されると、改良ステップによってサブピクセル解像度を実現できます。

結果と考察

Ni パターン

Spherical Indexingは、広範囲のパターン品質を持つEBSDパターンに使用することができます。この例では、適切に研磨されたニッケル合金の同じ領域に対して、異なるカメラゲインでEBSD分析を行い、意図的にシグナルノイズ比の良質なパターンと低質なパターンを得ました。その後、Spherical Indexingを行い、標準的なHough変換の指数付けと比較することで、Spherical Indexingがシグナルノイズ比が低いパターンに対しても、従来の指数付けと比較して、より高品質なデータを取得できることを説明します。

図 1. a)高クオリティーパターンの指数付け結果　b)バンド幅63とオイラーグリッド１２８におけるSpherical Indexing結果 c) バンド幅63におけるrefine結果

図１は、a)高SNRパターンの指数付け結果、b) バンド幅63とオイラーグリッド１２８におけるSpherical Indexing結果（refine無し）、ｃ）バンド幅63におけるrefine結果を示す。グリッドポイントの間隔は～2.8° (360° / 128) であるため、refine無しの結果は、方位が不連続で段差があるように見えることに注意してください。 refine後、どのような方位にも対応し、滑らかな結果が得られます。

図 2. a) 0°、b) 1°、c) 2°で同じ領域を示したKAMマップ

図 2 では、同じ領域の KAM マップが a) 0°、b) 1°、c) 2° で示されています。 refine無しの場合、パッチ内に方位のずれがなく、それらの間に鋭いスパイクがないことに注意してください。 Hough変換の指数付けとrefine後のSpherical Indexingはどちらも滑らかに見えますが、KAM を使用すると、Hough変換の指数付けのわずかな方位ノイズが見られます。

図 3. 低クオリティーのパターンでは、Hough変換の指数付けは a) 最初から失敗しますが、b) Spherical Indexingは確かなソリューションを提供し、c) refine後の連続的な方位勾配を正確に表示します。

低クオリティーのパターンでは、Hough変換の指数付けは a) 最初から失敗しますが、b) Spherical Indexingは確かなソリューションを提供し、c) refine後の連続的な方位勾配を正確に表示します。

図 4. バンド幅a) 63、 b) 95、c) 127を、(a – c) および refine後の(d – f)で比較します。

非常に低い SNR パターンの場合、指数付け結果を改善するには、より高いバンド幅が必要になる場合があります。図 4 では、a) 63、b) 95、および c) 127 のバンド幅が、(a – c) およびrefine後の (d – f) と比較されています。 refine前の方位の個別のステップは、オイラー角グリッドの解像度が高くなるにつれて小さくなりますが、同様の方位にrefineされることに注意してください。 3 つのバンド幅すべてで、グリッドサイズは 2 * (バンド幅 + 1) です。

図 5. a) 生のパターン、b) Hough変換の指数付けを使用した NPAR パターン、c) 生のパターン、d) バンド幅 127 でSpherical Indexingを使用した NPAR パターン

OIM Analysisに統合されたSpherical Indexingにより、既存の画像処理アルゴリズムを特に難しいパターンに使用できます。非常に高いノイズレベルでは、Hough変換指数付けはどのポイントにも指数付けることができず、Spherical Indexingはいくつかのポイントで失敗し始めます。 NPAR は、各パターンを隣接するパターンと平均化し、空間分解能と引き換えにパターン品質を向上します。改善されたパターンは、両方の方法で確実に指数付けできますが、Hough変換の指数付けでは、粒界付近で生じる重複パターンに苦労します (図 5)。.

熱間圧延Mg

図 6. a) 大きな変形によってパターンの品質が低下した場合、Hough変換の指数付けに苦労しますが、b) Spherical Indexingはパターンの品質が大幅に低下した場合に有効です。 d) Spherical Indexingの信頼性指数は、c) Image Qualityと強く相関しますが、IQ が非常に低い一部の領域においても高くなっています。

マグネシウムは、後方散乱信号が低い軽元素であるため、EBSD パターンの SNR 値が低く、EBSD 分析が困難になる可能性がある材料となります。マグネシウムの試料が変形すると、結果として生じる格子の歪みが全体的なパターンの品質を低下させるため、より難易度が高くなります。 Hough変換による指数付けは、これらのタイプのパターンの指数付けに苦労します (a) が、Spherical Indexingは、大幅に劣化したパターン品質に対して有効であり (b)、変形レベルが増加するにつれてより良い指数付けを可能にします。 d) Spherical Indexingの信頼性指数は、c) Image Qualityと強く相関しますが、IQ が非常に低い一部の領域のいても高くなっています (図 6)。

変形二相鋼

図 7. 相の識別は、二相鋼の相の類似性に依存します。 d – f) Spherical Indexingと a – c) Hough変換の指数付けによる方位結果の品質に加えて、b – c と e – f) 相の識別は、Spherical Indexingにおいて BCC と FCC の鉄が十分に分離できることで改善されます。

これまでの例では、SNR値の低下や試料変形の増大によりEBSDパターンの品質が低下した場合に、Spherical IndexingによりEBSDパターンの指数付けを改善する方法を示しました。この例では、変形した多相試料に対してSpherical Indexingを行っており、多相の場合でも指数付けの改善が可能であることを示しています。Spherical Indexingは、他の指数付け手法と同様に、多相に適用することが可能です。相の識別は、図7に示す二相鋼との相の類似性に依存します。d-f) Spherical Indexingとa-c)Hough変換の指数付けの方位結果の品質に加え、b-cとe-f)BCCとFCC鉄はよく分離され、相の識別が改善されました。特に困難なケースでは、Spherical Indexingのrefineが必要な場合があります。

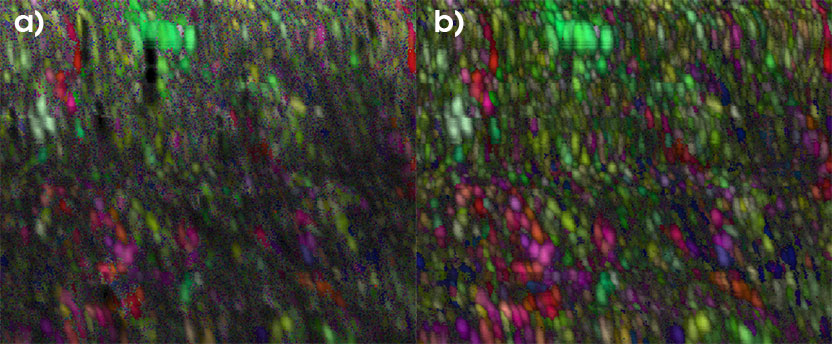
図 8. a) Spherical CI＋IPFは、b) Hough　IQ＋IPFと同様の傾向を示す

繰り返しになりますが、Spherical Indexingの信頼性指数はパターンの品質とよく相関しています。図 8 では、a) Spherical CI + IPF は、b) Hough IQ + IPF と同様の傾向を示しています。

まとめ

フォワードモデルの指数付けは、ユーザーがデータから抽出した情報を最大限に活用することを可能にしますが、これまでの学習曲線は急勾配でした。Hough変換の指数付けはよく確立されていますが、パターンの質の低さに影響されます。Sphericalベースの指数付けは、フォワードモデルの指数付けの堅牢性とHough変換の指数付けのスピードと使いやすさを兼ね備えています。

参考文献

Callahan, P. G., & De Graef, M. (2013). Dynamical electron backscatter diffraction patterns. Part I: Pattern simulations. Microscopy and Microanalysis, 19(5), 1255-1265.
Callahan, P. G., & De Graef, M. (2013). Dynamical electron backscatter diffraction patterns. Part I: Pattern simulations. Microscopy and Microanalysis, 19(5), 1255-1265.
Lenthe, W. C., Singh, S., & De Graef, M. (2019). A spherical harmonic transform approach to the indexing of electron backscattered diffraction patterns. Ultramicroscopy, 207, 112841.
Hielscher, R., Bartel, F., & Britton, T. B. (2019). Gazing at crystal balls: Electron backscatter diffraction pattern analysis and cross-correlation on the sphere. Ultramicroscopy, 207, 112836.
Sparks, G., Shade, P. A., Uchic, M. D., Niezgoda, S. R., Mills, M. J., & Obstalecki, M. (2021). High-precision orientation mapping from spherical harmonic transform indexing of electron backscatter diffraction patterns. Ultramicroscopy, 222, 113187.