Skip to content
日本語
Search

OIM AnalysisにおけるSpherical Indexing

はじめに

電子線回折結晶方位解析(EBSD)の中核をなすのが、パターンの指数付けです。EBSDの自動化の鍵は、効果的な指数付けアルゴリズムの開発にあり、これは2つのステップで達成されました：(1) Hough変換によるパターン中のバンドの検出1 (2) 結晶方位を決定するために、検出されたバンド間の角度を結晶格子の面間角度と比較2 。このアプローチは、長年にわたってうまく機能してきました。

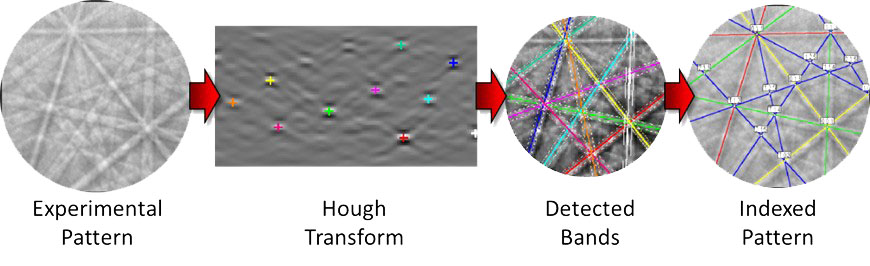
Houghに基づく指数付けの概略
図 1. Houghに基づく指数付けの概略

そして今、新世代の指数付けが登場しました。この新しい指数付けアプローチの鍵は、ダイナミックな回折モデル3, 4 を用いて EBSD パターンを正確にシミュレートする能力です。この新しい指数付けアプローチは、パターンマッチングアプローチを用いており、最初のステップは、パターンまたはあらゆる可能性のある方位の「dictionary」を構築することです。実際の指数付けは、実験パターンをdictionaryのすべてのパターンと比較して、最もよく一致するものを見つけることによって行われます5 。ご想像の通り、これはかなりコンピュータの集約的な指数付け手法となります。この技法はOIM Analysis™に実装され、GPUを使用するようにコード化されているため、dictionary指数付け作成技法の応用が可能です。

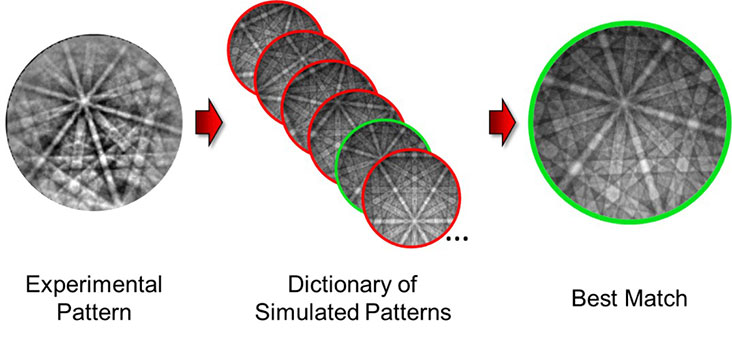
Dictionary Indexingの概略
図 2. Dictionary Indexingの概略

議論

Spherical Indexing6, 7と呼ばれる、より効率的なアプローチがOIM Analysis 9に実装されたことを発表できることを大変嬉しく思います。数学的な背景はかなり複雑ですが、コンセプトはそれほど難しくありません。先程、すべての方位についてdictionaryを計算すると述べました。もちろん、これは正確には正しくありません。方位空間は有限の方位の集合に離散化され、この離散化された方位空間に対してパターンがシミュレートされます。しかし、方位空間を球体として考える方法もあります。各方位におけるすべてのパターンをシミュレートする代わりに、単一の球状のパターンをシミュレートすることができます。次のステップは、球面上に実測パターンを逆投影し、相互相関を使用して（球面調和関数など）球面パターンへの最適なフィットを見つけることです。このアプローチもGPUを使用し、現在のHough変換/3バンド指数付けアプローチの速度に匹敵する指数付け速度を達成可能で、Houghベースの方法よりも堅牢性が高くなっています。


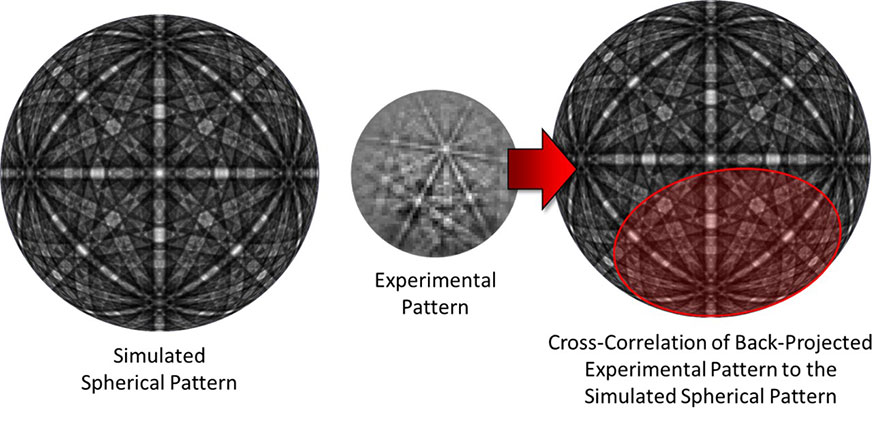
図 3. Spherical Indexingの概略

Spherical Indexingは、高度に変形した材料、回折パターンの発生が弱い材料、粗い表面を持つ試料など、従来の指数付けが苦手とする試料に非常に効果的です。図4は、ショットピーニングされたアルミニウム試料の断面の例を示しています。Houghベースの指数付けよりも指数付けされた点の数、およびDictionary Indexingによって得られたものよりも方位勾配の連続性という点で、指数付け性能が向上していることに注目してください（例えば、底部付近のマップの右端にあるピンク色の粒）。

Hough変換ベース、Dictionary Indexing、Spherical Indexingによっての指数付けしたショットピーニングされたアルミニウム試料の方位マップ
図 4. Hough変換ベース、Dictionary Indexing、Spherical Indexingによっての指数付けしたショットピーニングされたアルミニウム試料の方位マップ

詳細については、OIM解析におけるSpherical Index法と実空間refinementを用いたEBSD 指数付け課題の克服ウェビナーやSpherical Indexingアプリケーションノートをご覧ください。

参考文献

  1. NC Krieger Lassen, D Juul Jensen & K Conradsen (1992) “Image processing procedures for analysis of electron back scattering patterns”, Scanning Microscopy, 6, 115-121
  2. SI Wright, & BL Adams (1992) “Automatic analysis of electron backscatter diffraction patterns”, Metallurgical Transactions A, 23, 759-767.
  3. A Winkelmann, C Trager-Cowan, F Sweeney, AP Day, & P Parbrook (2007) “Many-beam dynamical simulation of electron backscatter diffraction patterns”, Ultramicroscopy, 107, 414-421.
  4. PG Callahan & M De Graef (2013) “Dynamical electron backscatter diffraction patterns. Part I: Pattern simulations”, Microscopy and Microanalysis, 19,1255-1265.
  5. SYH Chen, SU Park, D Wei, G Newstadt, MA Jackson, JP Simmons, M De Graef & AO Hero (2015) “A dictionary approach to electron backscatter diffraction indexing”, Microscopy and Microanalysis, 21, 739-752
  6. R Hielscher, F Bartel & B Britton (2019) ”Gazing at crystal balls: Electron backscatter diffraction pattern analysis and cross correlation on the sphere”, Ultramicroscopy, 207, 112836.
  7. WC Lenthe, S Singh, & M De Graef (2019). A spherical harmonic transform approach to the indexing of electron back-scattered diffraction patterns. Ultramicroscopy, 207, 112841.